- 家計管理
-
毎月の支出を記録し、標準偏差を計算することで、どの月が特に費用がかさんでいるか、または安定しているかをご確認いただけます。
- 健康管理
-
毎日の体重や睡眠時間を標準偏差で分析することで、習慣がどの程度安定しているかをご確認いただけます。
- 運動の成果測定
-
ランニングタイムや歩数のデータを記録し、標準偏差を計算することで、運動量がどれくらい安定しているかを確認することが可能です。
- 学習の進捗評価
-
テストの点数や学習時間の記録を分析し、標準偏差を利用して成果がどれくらい安定しているかをご確認いただけます。
| 行番号 | 入力値 | 平均値 |
|---|---|---|
|
標準偏差の活用ガイド:
±1標準偏差: 平均値 ± 標準偏差 (約68.3%) ±2標準偏差: 平均値 ± (標準偏差×2) (約95.4%) ±3標準偏差: 平均値 ± (標準偏差×3) (約99.7%) |
||
| 標準偏差 | 0.00 | |
| 範囲 (±1σ) | — | |
| 範囲 (±2σ) | — | |
| 範囲 (±3σ) | — | |
正規分布と標準偏差の関係 データが正規分布(山の形の分布)に従う場合、標準偏差を使ってデータの広がりを測定します。正規分布では、データは「平均値(中心)」を基準として広がり、以下のような割合でデータが分布します:
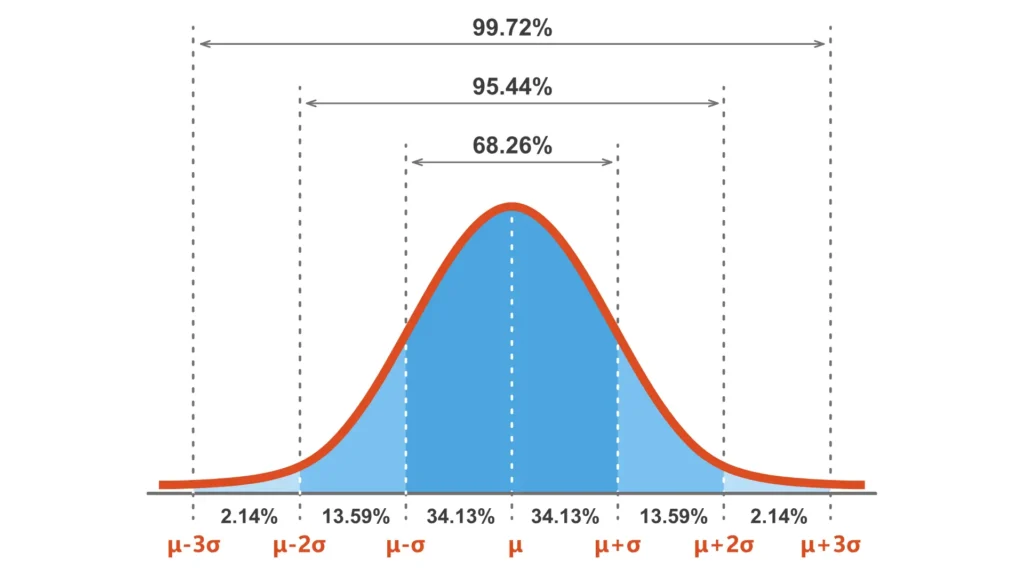
- 平均 ±1標準偏差の範囲 全体の約68.26%のデータがこの範囲に収まります。 例えば、平均が50、標準偏差が10の場合、「40~60」の範囲に大部分のデータが存在します。
- 平均 ±2標準偏差の範囲 全体の約95.44%のデータがこの範囲に収まります。 先ほどの例でいうと、「30~70」の範囲ですね。この広がりでは、さらに多くのデータを含みます。
- 平均 ±3標準偏差の範囲 全体の約99.73%のデータがこの範囲に収まります。 極端な値以外、ほとんどすべてのデータがこの範囲内に含まれます。例えば、「20~80」の範囲です。
イメージで理解 正規分布を山に例えると、山の真ん中が「平均値」で、標準偏差はその山の横幅を決めます。標準偏差が小さいと山はスリムになり、大きいと広がった山になります。そして、この山のそれぞれの幅にどの程度のデータが含まれているのかをパーセンテージで示すのが「68.26%、95.44%、99.73%」の数字です。

